Quick sort

Overview

Quicksort is an algorithm of reorder a list in ascending order.
Quicksort uses the concept of the divide and conquer algorithm.

Quick sort main idea

The main idea of quicksort is to pick an element as a pivot and partition the array around the pivot. When we partition the array we sort the elements in a manner way to make all small elements before the pivot and all the greatest elements after the pivot, this is the core of the partition part.

What does pivot mean?

Pivot is the value within the partitioning space that I want to find a position for.

What does the i variable do?

Remember the last position that an element was placed in, that was less than the pivot.

What does the j variable do?

Scan from left boundary to right - 1 boundary.

How to pick the pivot?

There are many different ways of picking the pivot:
1. Always pick the first element as a pivot.
2. Always pick the last element as a pivot.
3. Pick a random element as a pivot.
4. Pick median as the pivot.

In this article, I will pick the last element as a pivot. Other ways of picking pivot have a slightly different implementation.

Pseudoscope

ALGORITHM QuickSort(arr, left, right)
    if left < right
        DEFINE position <-- Partition(arr, left, right)
        QuickSort(arr, left, position - 1)
        QuickSort(arr, position + 1, right)

ALGORITHM Partition(arr, left, right)
    DEFINE pivot <-- arr[right]
    DEFINE i <-- left - 1
    for j <-- left to right do
        if arr[j] <= pivot
            i++
            Swap(arr, i, j)

     Swap(arr, i+1, right)
     return i + 1

ALGORITHM Swap(arr, i, j)
    DEFINE temp;
    temp <-- arr[i]
    arr[i] <-- arr[j]
    arr[j] <-- temp

Code implementation

def quick_sort(arr, left, right):
    if left < right:
        position = partition(arr, left, right)
        quick_sort(arr, left, position-1)
        quick_sort(arr, position+1, right)


def partition(arr, left, right):
    pivot = arr[right]
    i = left - 1
    for j in range(left, right):
        if arr[j] <= pivot:
            i += 1
            swap(arr, i, j)

    swap(arr, i+1, right)
    return i+1


def swap(arr, i, j):
    temp = arr[i]
    arr[i] = arr[j]
    arr[j] = temp

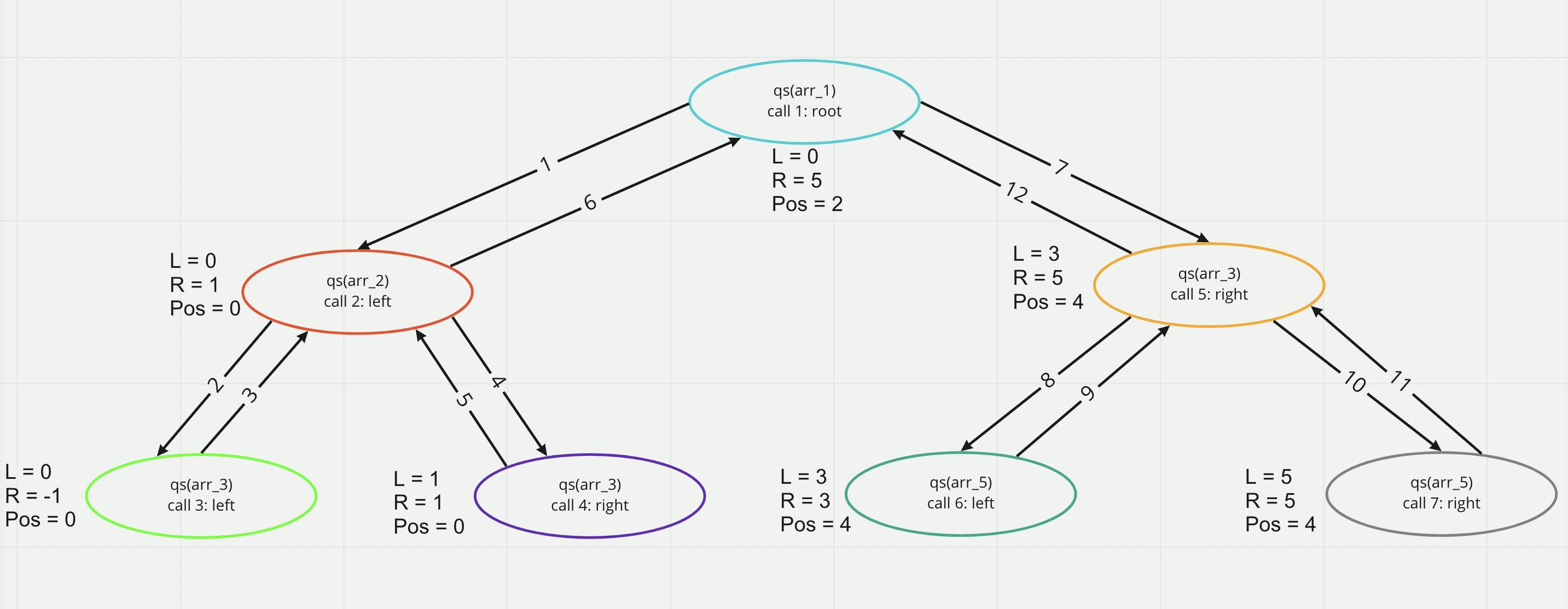
Let's trace the code

Assume this sample array [8, 4, 23, 42, 16, 15]

Check the images below for step by step tracing:

Efficiency

Time Big-O(n²)
Space Big-O(n)

Recources

Nour Eddein's Blog